One Effective Method for Solving Singularly Perturbed Equations

Abstract

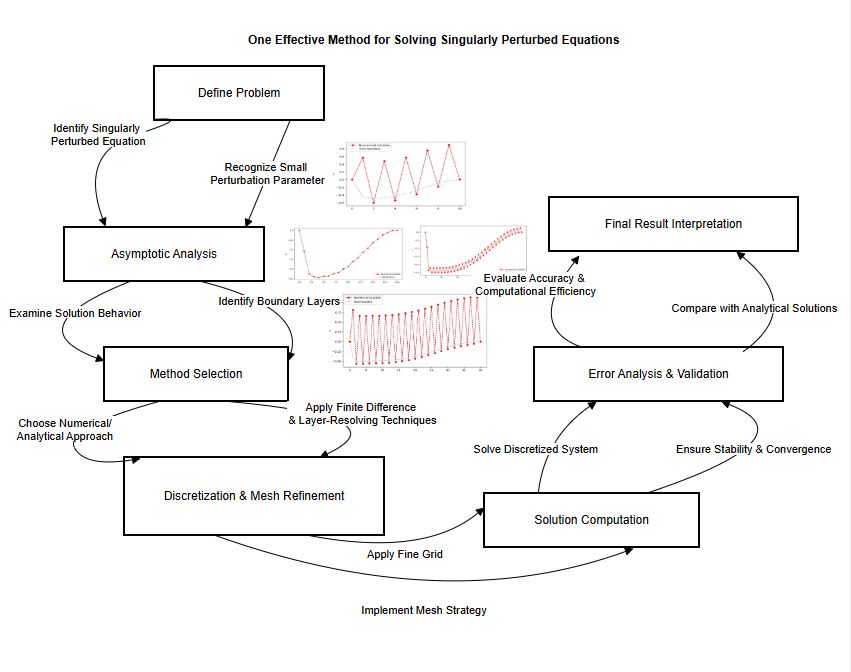
Numerical methods are widely used to study the solution of singularly perturbed equations. At the same time, their application to the solution of such equations encounters serious difficulties; they are associated with the presence of a small parameter at the highest derivative and the appearance in the solution area of ​​areas with high frequency-amplitude sawtooth jumps. In this case, the requirements for the efficiency and accuracy of numerical methods increase sharply. Although numerous methods have been developed to date, the question of the effectiveness and accuracy of numerical methods remains open.

Until now, different methods with uniform and non-uniform steps have been mainly used to solve singularly perturbed equations. As the value of the small parameter decreases, to increase the accuracy, it is necessary to refine the step of the difference grid. This, in turn, leads to a strong increase in the order of the matrix in the linear algebraic system being solved. Along with difference methods, spectral methods can be used to solve problems. In spectral methods, the solution to the equation is sought in the form of finite series in Chebyshev polynomials. The derivatives present in the equation are determined by differentiating the selected final series. When differentiating series, the order of the approximating polynomials is reduced, and this, in turn, affects the accuracy of the method used.

In this paper, it is proposed to use the preliminary integration method to solve singularly perturbed equations. The essence of this method is as follows. The highest derivative and the right-hand side of the differential equation are expanded into finite series in Chebyshev polynomials of the first kind. Unlike spectral methods, in the preliminary integration method the highest derivative is expanded into a finite series. Before solving the problem, the series for the highest derivative is preliminarily integrated until an expression for solving the problem is found in the form of a finite series. When integrating series, unknown integration constants appear; they are determined from additional conditions of the problem. Only after this, the series for solving the derivatives of the right side are put into a singularly perturbed equation and a system of linear algebraic equations is obtained for determining the unknown expansion coefficients. It should be noted that when integrating series, the smoothness of the approximating polynomials improves, and this, in turn, increases the accuracy of the proposed method. At the same time, the order of the matrix of the algebraic system being solved does not increase. This ensures, at the same costs required in the spectral method, that the proposed method can solve a singularly perturbed equation even for small values ​​of the small parameter of the problem. The high accuracy and efficiency of the preliminary integration method are demonstrated when solving a specific inhomogeneous singularly perturbed equation. The results of calculations are presented by comparing the approximate solution with the exact solution of the problem and with approximate solutions obtained by the spectral method.