On the Kronecker Structure of linearization of Cubic Two-Parameter Eigenvalue Problems

Article Sidebar

PDF
Published: Mar 28, 2025
DOI: https://doi.org/10.22452/mjs.vol44no1.9
Keywords:
Cubic two-parameter eigenvalue problem, Linear two-parameter eigenvalueproblem, linearization, matrix polynomial.

Main Article Content

Niranjan Bora
Department of Mathematics, Dibrugarh University Institute of Engineering and Technology Assam-786004, INDIA.
https://orcid.org/0000-0002-3729-5848
Bharati Borgohain
Department of Mathematics, Dibrugarh University, Assam-786004, INDIA.
https://orcid.org/0009-0007-3475-5267

Abstract

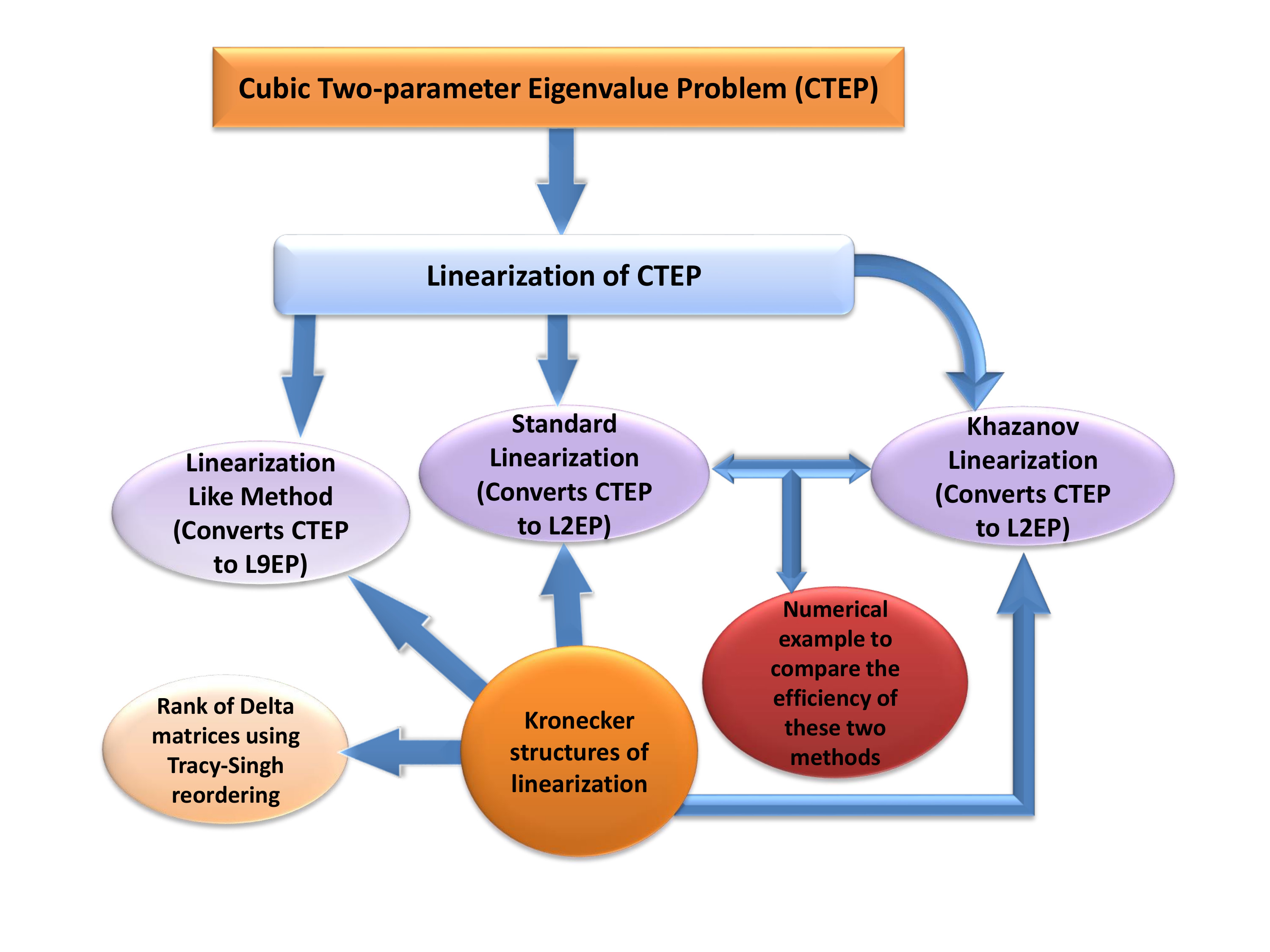
Linearization is a classical approach to study matrix polynomial of the form P(lambda)=Sum lambdaj Aj, where A j Cnxn .  It converts  into a matrix pencil of the form L(lambda)=A+lambda B  of high dimension, where A and B are matrices over C , and lambda is the spectral parameter. In this paper we consider Cubic two-parameter eigenvalue problems ( CTEP) and study three different linearization process of the problem. Usinglinearization techniques, CTEP  is first converted into a linear two-parameter eigenvalue problem(L2EP)  of coefficient matrices of different sizes. The main advantage of these linearizations lies in the fact that, after transforming them into suitable linearized forms, existing numerical techniques for linear multiparameter eigenvalue problems (LMEP)  can be applied to CTEP  without solving the original problem. While solving  CTEP by formulating suitable linearizations, several transformations are generally used. In the current paper, it is also intended to report on these transformations, which have not been studied completely due to the complexity of their Kronecker structures.

Downloads

Download data is not yet available.

Article Details

How to Cite
Bora, N., & Borgohain, B. (2025). On the Kronecker Structure of linearization of Cubic Two-Parameter Eigenvalue Problems. Malaysian Journal of Science, 44(1), 70–86. https://doi.org/10.22452/mjs.vol44no1.9
Issue
Vol 44 No 1 (2025): March 2025
Section
Original Articles
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Transfer of Copyrights

  •  In the event of publication of the manuscript entitled [INSERT MANUSCRIPT TITLE AND REF NO.] in the Malaysian Journal of Science, I hereby transfer copyrights of the manuscript title, abstract and contents to the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) for the full legal term of copyright and any renewals thereof throughout the world in any format, and any media for communication.

 

Conditions of Publication

  •  I hereby state that this manuscript to be published is an original work, unpublished in any form prior and I have obtained the necessary permission for the reproduction (or am the owner) of any images, illustrations, tables, charts, figures, maps, photographs and other visual materials of whom the copyrights is owned by a third party.
  • This manuscript contains no statements that are contradictory to the relevant local and international laws or that infringes on the rights of others.
  • I agree to indemnify the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) in the event of any claims that arise in regards to the above conditions and assume full liability on the published manuscript.

 

Reviewer’s Responsibilities

  • Reviewers must treat the manuscripts received for reviewing process as confidential. It must not be shown or discussed with others without the authorization from the editor of MJS.
  • Reviewers assigned must not have conflicts of interest with respect to the original work, the authors of the article or the research funding.
  • Reviewers should judge or evaluate the manuscripts objective as possible. The feedback from the reviewers should be express clearly with supporting arguments.
  • If the assigned reviewer considers themselves not able to complete the review of the manuscript, they must communicate with the editor, so that the manuscript could be sent to another suitable reviewer.

 

Copyright: Rights of the Author(s)

  • Effective 2007, it will become the policy of the Malaysian Journal of Science (published by the Faculty of Science, University of Malaya) to obtain copyrights of all manuscripts published. This is to facilitate:
  • Protection against copyright infringement of the manuscript through copyright breaches or piracy.
  • Timely handling of reproduction requests from authorized third parties that are addressed directly to the Faculty of Science, University of Malaya.
  • As the author, you may publish the fore-mentioned manuscript, whole or any part thereof, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given. You may produce copies of your manuscript, whole or any part thereof, for teaching purposes or to be provided, on individual basis, to fellow researchers.
  • You may include the fore-mentioned manuscript, whole or any part thereof, electronically on a secure network at your affiliated institution, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
  • You may include the fore-mentioned manuscript, whole or any part thereof, on the World Wide Web, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
  • In the event that your manuscript, whole or any part thereof, has been requested to be reproduced, for any purpose or in any form approved by the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers), you will be informed. It is requested that any changes to your contact details (especially e-mail addresses) are made known.

 

 Copyright: Role and responsibility of the Author(s)

  • In the event of the manuscript to be published in the Malaysian Journal of Science contains materials copyrighted to others prior, it is the responsibility of current author(s) to obtain written permission from the copyright owner or owners.
  • This written permission should be submitted with the proof-copy of the manuscript to be published in the Malaysian Journal of Science  

Licensing Policy

Malaysian Journal of Science is an open-access journal that follows the Creative Commons Attribution-Non-commercial 4.0 International License (CC BY-NC 4.0)

CC BY – NC 4.0: Under this licence, the reusers to distribute, remix, alter, and build upon the content in any media or format for non-commercial purposes only, as long as proper acknowledgement is given to the authors of the original work. Please take the time to read the whole licence agreement (https://creativecommons.org/licenses/by-nc/4.0/legalcode ).

References

Atkinson FV. (1972). Multiparameter eigenvalue problems, Academic Press, New York.

Bueno MI., Dopico FM., Furtado S., MedinaL. (2018). A block-symmetric linearization of odd degree matrix polynomials with optimal eigenvalue condition number and backward error, Calcolo, 55: 32.

CoxD., Little J., O’shea D. (1998).Using Algebraic Geometry, Springer Verlag, New York.

Das RK., Alam R. (2019). Automatic recovery of eigenvectors and minimal bases of matrix polynomials from generalized Fiedler pencils with repetition, Linear Algebra Appl. 569, 78-112.

Das B.(2020). Linearizations and distance problems associated with matrix polynomials, Ph.D. thesis, IIT Guwahati, India.

Dmytryshyn A., Johansson S., Kagström B., DoorenPV. (2020).Geometry of Matrix Polynomial Spaces, Foundations Comput. Math. 20, 423-450.

Dong B. (2022). The Homotopy Method for the Complete Solution of Quadratic Two-parameter Eigenvalue Problems, J. Scientific Comput. 90:18.

DoorenPV. (1997). The computation of Kronecker’s canonical form of a singular pencil, Linear Algebra Appl. 27, 103-141.

GohbergI., LancasterP., RodmanL. (2009). Matrix Polynomials, Society for Industrial and Applied Mathematics, Philadelphia.

Henderson HV., Pukelsheim F., Searle SR. (1983).On the history of the kronecker product, Linear Multilinear Algebra 14, 113-120.

Higham NJ., Mackey D.S., Tisseur F.O. (2006).The Conditioning of Linearizations of Matrix Polynomials, SIAM J. Matrix Anal. Appl. 28(4), 1005-1028.

Hochstenbach ME., Muhič A., Plestenjak B. (2012). On linearizations of the quadratic two-parameter eigenvalue problems, Linear Algebra Appl. 436(8), 2725-2743.

Hochstenbach ME., Kosir T., Plestenjak B. (2005). A Jacobi-Davidson type method for the nonsingular two-parameter eigenvalue problem, SIAM J. Matrix Anal. Appl. 26, 477-497.

Hochstenbach ME., MuhičA., Plestenjak B. (2015)Jacobi–Davidson methods for polynomial two-parameter eigenvalue problems, J. Comput. Applied Math. 288, 251-263.

Hochstenbach ME., Košir T., Plestenjak B. (2005)A Jacobi-Davidson type Method for nonsingular two-parameter eigenvalue problem,SIAM J. Matrix Anal. Appl. 26(2), 477-497.

Hochstenbach ME., Muhič A., Plestenjak B. (2015)Jacobi-Davidson methods for polynomial two-parameter eigenvalue problems, J. Comput. Applied Math. 288, 251-263.

Jarlebring E., Hochstenbach ME. (2009). Polynomial two-parameter eigenvalue problems and matrix pencil methods for stability of delay-differential equations, Linear Algebra Appl. 431, 369–380.

Khazanov VB. (2007). To solving spectral problems for multiparameter polynomial matrices, J. Math. Sci. 141, 1690-1700.

Košir T., Plestenjak B. (2022).On the singular two-parameter eigenvalue problem II*. Linear Algebra Appl. 649, 433-451.

Kressner D., Glibić IŠ. (2023). Singular quadratic eigenvalue problems: Linearization and weak condition numbers, BIT Numer. Math., Article no. 18.

Lancaster P. (2008). Linearization of regular matrix polynomials, Elect. J. Linear Algebra. 17, 21-27.

Lancaster P., Zaballa I. (2021).Spectral theory for self-adjoint quadratic eigenvalue problems - a review, Elect. J. Linear Algebra. 37, 211-246.

Mackey DS., Mackey N., Mehl C., Mehrmann V. (2006). Vector Spaces of Linearizations for Matrix Polynomials, SIAM J. Matrix Anal. Appl. 28(4), 971-1004.

Meerbergen K., Schröder C., Voss H. (2013). A Jacobi-Davidson method for two-real-parameter nonlinear eigenvalue problems arising from delay-differential equations, Numer. Linear Algebra Appl. 20(5), 852–868.

Muhič A., Plestenjak B. (2009). On the singular two-parameter eigenvalue problem, Elect. J. Linear Algebra 18, 420-437.

Muhič A., Plestenjak B. (2010). On quadratic two-parameter eigenvalue problems and its linearization,Linear Algebra Appl. 432, 2529-2542.

PlestenjakB. (2016).Numerical methods for nonlinear two-parameter eigenvalue problems, BIT Numer. Math. 56, 241–262.

Plestenjak B. (2017). Minimal determinantal representations of bivariate polynomials, Linear Algebra Appl. 532, 550–569.

Plestenjak B., Hochstenbach ME. (2016). Roots of bivariate polynomial systems via determinantal representations, SIAM J. Scientific Comput. 38, A765–A788.

Tisseur F., Meerbergen K. (2001).The Quadratic Eigenvalue Problem, SIAM Rev. 43(2), 235-286.